Lo primero que tenemos que comprender es que, al contrario de lo que ocurría en las curvas sencillas de nuestra primera entrega, en este tipo de curvas entran en juego formas geométricas complejas: curvas que van precedidas de otra curva, ya sea en el mismo sentido, o en el contrario. Para todos estos casos, siempre debemos tener presente que la parte final de la sección es la que va a tener prioridad sobre las anteriores.
Esto sucede por una razón sencilla: la parte inicial del tramo la podemos planificar con antelación, y en cambio la salida final será el resultado de la trayectoria y velocidad con la que vengamos de todo lo anterior y, por tanto, nuestra capacidad de rectificación es mucho menor. Por eso trataremos de poner toda la trazada de la primera parte al servicio de la segunda para llegar a buen puerto.
Aquí encontramos la primera idea que viene de los rallyes: "Sacrificar" una curva. Luis Moya, copiloto de Carlos Sáinz solía indicarlo frecuentemente con el término "sasa" (para abreviar en la locución), y con ello indicaba al piloto que la primera curva debía sacrificarla para salvar así la siguiente.
Con la siguiente ilustración comprenderemos mejor la idea. Se trata de una sección de curvas enlazadas, la primera a la derecha y la segunda a la izquierda:
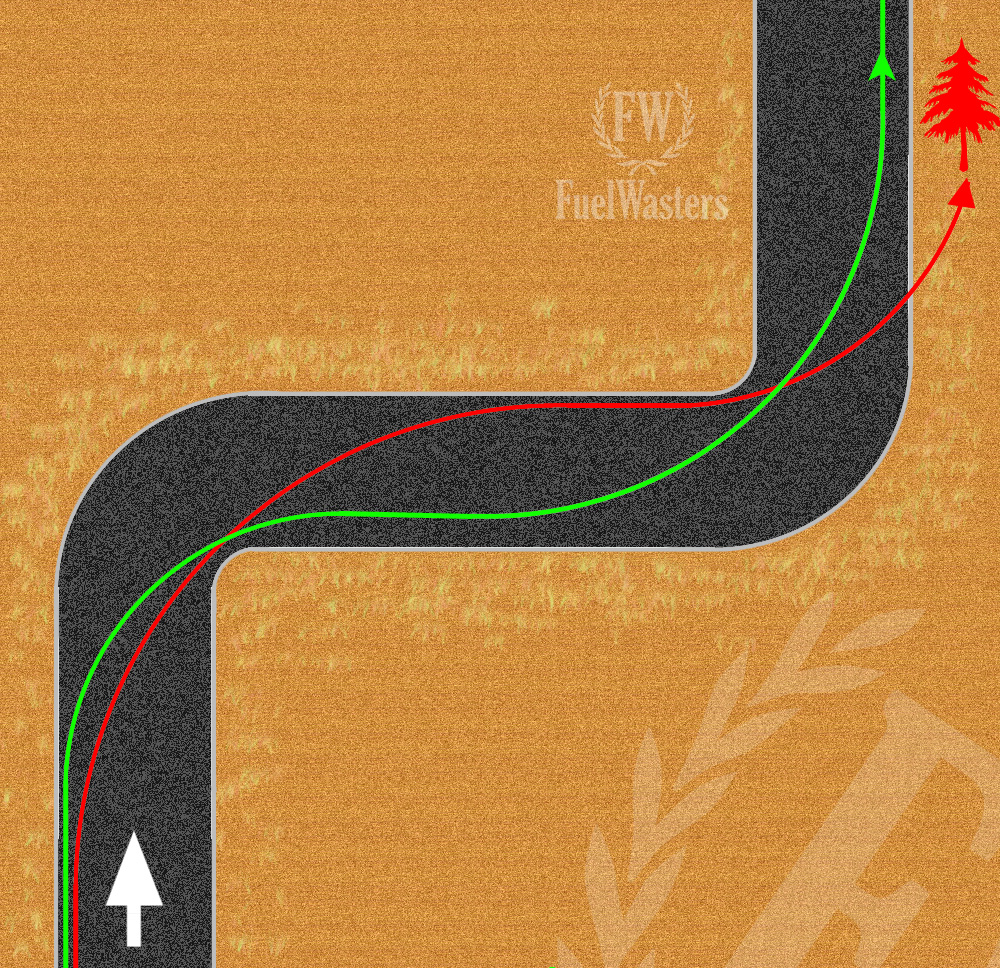
Como se puede observar, la trazada roja es la que haríamos si no tuviéramos en cuenta la segunda curva, y sería la línea óptima para trazar la primera sección de forma aislada: entramos por fuera, "picamos" hacia el interior, y salimos por fuera, describiendo la máxima parábola posible, como ya vimos en el primer volumen sobre curvas.
Pero al tener después una curva opuesta, en lugar de encontrarnos ahora en el exterior para trazarla, nos vemos lanzados desde el interior, sin margen para trazar bien la misma parábola que en la primera.
Los resultados dependerán de la velocidad por la que hayamos pasado anteriormente, de la capacidad de corrección del coche, y de la destreza del conductor, pero desde luego, huelga decir que la situación pinta bastante mal llegados a este punto...
Por el contrario, para las enlazadas propuestas la trazada verde es la correcta. Estamos suponiendo que se conoce con antelación la sección completa, y por eso sacrificamos la primera trazada en pro de la segunda. Se puede apreciar cómo la primera curva no se ha trazado de la forma más ortodoxa, ya que sale por dentro en lugar de por fuera, pero todo cobra sentido cuando vemos que es desde ese punto desde el que (ahora sí) podemos trazar correctamente la segunda, con un mayor ángulo, y saliendo de la sección completa por la trazada correcta y más segura. Recordad que siempre damos prioridad a la última sección para salir airosos. En este ejemplo son dos curvas enlazadas, pero a veces pueden ser tres, y la técnica es la misma: sacrificar lo anterior para hacer correctamente lo último.
Curvas que se cierran
Otro caso complejo que se suele dar más de lo que debería en nuestras carreteras (especialmente en incorporaciones o salidas de autopistas), son las curvas de radio decreciente, aquellas de las que solemos decir que son "curvas que se cierran". Podemos entenderlo mejor si pensamos en ella como dos curvas consecutivas en el mismo sentido, siendo la primera más abierta que la segunda.
El problema, a grandes rasgos, vuelve a ser el mismo que encontrábamos con las enlazadas: si entramos trazando correctamente la primera sección, cuando nos encontremos con que la curva se cierra, nos veremos empujados hacia el exterior y sin posibilidad de corregir la trayectoria.
Por suerte, la solución también sigue siendo la misma: dar prioridad a la sección final sobre la inicial, sacrificando la primera trazada en pro de la segunda.
Este tipo de curvas se suelen dar en los circuitos para añadir un componente más técnico al trazado, y suponen un reto para los pilotos por lo difícil que resulta negociarlas a gran velocidad. Zonas como el llamado "Super 7" del madrileño circuito del Jarama, o la curva parabólica del final de Cheste son buenos ejemplos de este tipo de giros, y sitios donde los aficionados se suelen colocar para ver trompos y salidas de pista.
Para este tipo de curvas, los pilotos de competición suelen recurrir a diversas trazadas, porque según sus características técnicas cada tipo de coche se comporta de una manera diferente en estas trayectorias tan comprometidas. Nosotros hemos escogido esta, por ser la más conservadora y la que más se ajusta a todos los tipos de turismos convencionales.
Es la que se puede encontrar en la mayoría de manuales de conducción un poco avanzados, y aunque cada uno pueda ajustar los puntos de entrada, vértice y salida más a su gusto, la base sería la que describimos.
Veamos la gráfica de una curva de radio decreciente y la trazada que proponemos:
 Como vemos, la línea roja no obedece a la trazada lógica de una curva abierta, y parece que tarda más de lo normal en buscar el interior. Es normal, porque el interior en realidad está retrasado por la curva más cerrada que encontramos a continuación.
Como vemos, la línea roja no obedece a la trazada lógica de una curva abierta, y parece que tarda más de lo normal en buscar el interior. Es normal, porque el interior en realidad está retrasado por la curva más cerrada que encontramos a continuación.
Si buscásemos el vértice interior con antelación, como podría esperarse en una de radio sencillo, nos encontraríamos que al cerrarse la segunda parte de la curva ya no podríamos ir correctamente al exterior de la calzada, sino que nos iríamos rectos hacia la cuneta, y una vez más, tendremos que confiar en que pudiésemos corregir.
Además, la velocidad a la que entramos en una curva abierta es mayor que la que necesitamos para una curva cerrada y necesitaremos frenar en ese momento intermedio, con la dificultad que entraña frenar un coche en pleno apoyo (también hablamos de ello en nuestra primera entrega).
Por eso, una vez más, pensamos en solucionar la parte final y poner la inicial a su servicio: entramos muy abiertos, retrasando el vértice, y cuando ya vemos que efectivamente la curva se cierra (y en qué medida), buscamos ese interior y salimos por el lado correcto de nuestro carril.
En realidad, si vemos la trayectoria roja, está negociada como una única curva, ni tan abierta como la primera sección ni tan cerrada como la segunda, sino la óptima para atravesar la sección completa con la suavidad y facilidad de una única parábola.
Regla de oro
Para terminar, recordemos la regla de oro para trazar curvas complejas: la parte final prima sobre la inicial, tanto en trayectoria como en velocidad.
La razón es sencilla: es más fácil entrar más lento y más cerrado cuando aún tenemos tiempo para planificarlo, que entrar bien para la primera sección, y encontrarnos con la obligación de corregir en la segunda, ya sea la línea como la velocidad.
Y como dijimos en la anterior entrega, todo esto lo haremos siempre sin salirnos de nuestro carril. Puede parecer obvio pero, por desgracia, vemos todos los días en nuestras carreteras que no lo es tanto.
Lea más sobre técnicas de conducción y su vehículo en Fuelwasters
